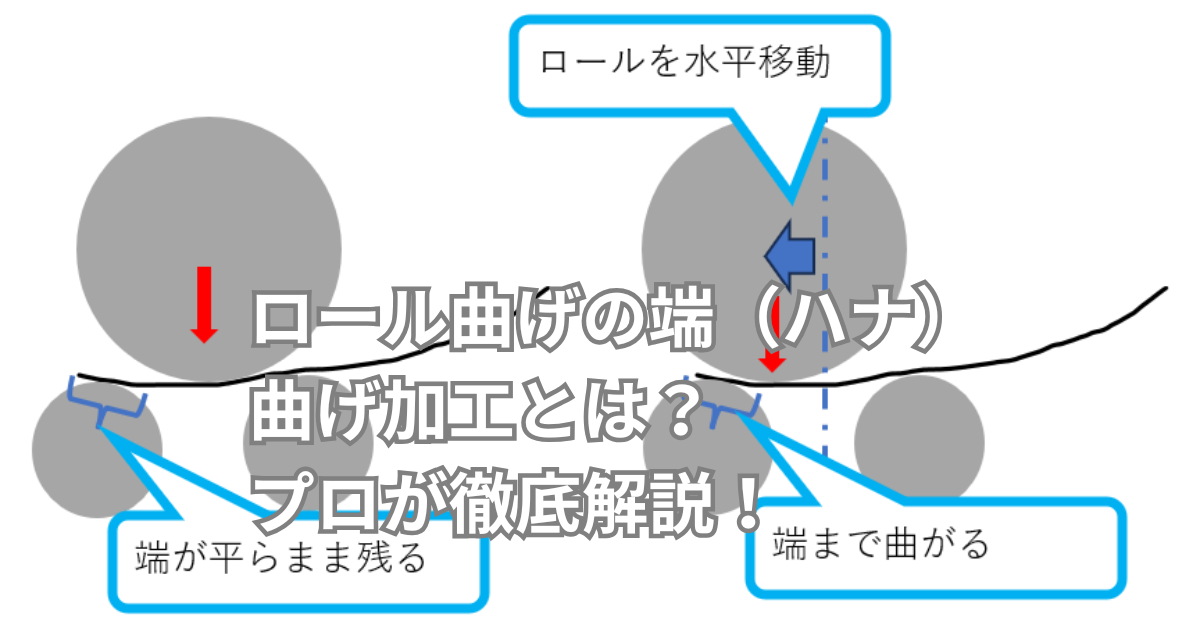
日常のあらゆる場面に潜む「角」の計算は、意外と必要な知識です。この記事では、a角、b角、c角といった基礎情報から、それらがどのように関連し合うか、さらには実生活での具体的な応用方法までを解説します。
図を使用しながら、誰もが理解しやすいように、複雑な計算テクニックを分かりやすく解説します。建築やデザイン、そして数学の学習に参考となる情報を含むので、ぜひ最後までご覧ください。
a角、b角、c角の基礎知識
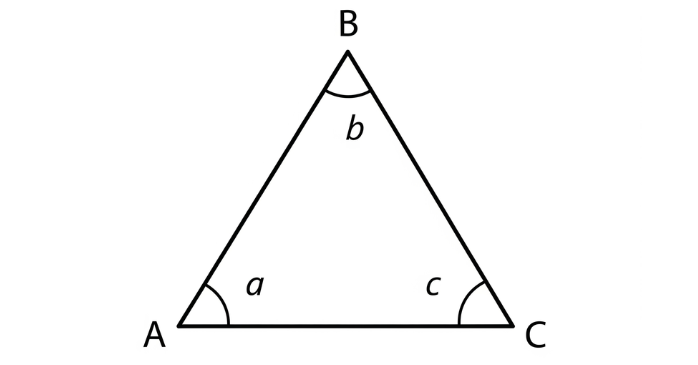
「a角」「b角」「c角」という角に関する基礎知識を解説します。これらの概念は、幾何学や加工などの分野で必要不可欠な情報です。図を使用して、それぞれの種類や計算方法、そして互いの関連性を分かりやすく解説します。専門的な知識がなくても、角に関する情報を知っておくだけで、物事の理解が深まります。
a角とは何か
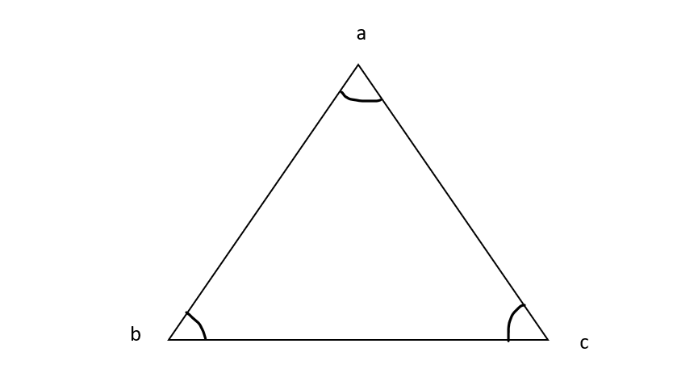
「a角」とは、三角形の3つの頂点のうち、Aと名付けられた頂点の角度を指します。 これは、数学や幾何学の分野で使用される基本的な定義です。たとえば、住宅の屋根の勾配を計算したり、デザインで安定した構図を考えたりする際に役立ちます。
b角の定義と特徴
「b角」は、三角形の3つの頂点のうち、頂点Bにある角度を指します。数学の問題や教科書では、どの角について話しているかを明確にするために、このように頂点の名前を使って角を区別します。
b角の大きさは、直角三角形、鋭角三角形、鈍角三角形といった三角形の種類によって様々です。たとえば、直角三角形ではb角が90度になることもありますし、二等辺三角形ではa角やc角と等しい値になることもあります。
このように、b角が他の角とどう異なるかを理解することは、三角関数の計算や図形の問題を解く上で非常に重要です。建築の設計やゲーム開発など、現実世界でも様々な場面でb角は使われており、その実用性は非常に高いです。
c角の計算方法
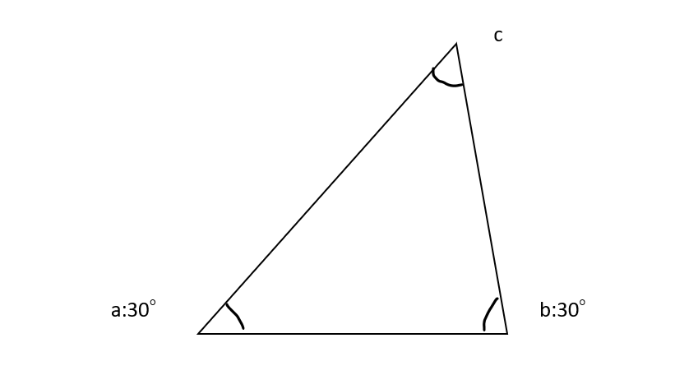
c角を求めるための計算方法はとても簡単です。三角形の内角の和は常に180°であるという技術を使います。
c=180∘−(30∘+70∘)=180∘−100∘=80∘
例題: a角が30°、b角が70°の場合、c角は何度になるでしょうか?
c=180∘−(30∘+70∘)=180∘−100∘=80∘
注意点: 計算する際は、すべての角度が同じ単位(度数法など)であることを確認しましょう。
金属加工における角の知識

金属加工における「角」は、単なる形状の一部ではなく、その種類や精度によって加工技術や製品の品質を大きく左右する重要な要素です。主に以下の3つの観点から知識を深めることができます。
角度の種類
角度は、製品の設計図に基づいてミリメートル単位で厳密に定義されます。主な角度の種類とそれに関わる加工技術は以下の通りです。
| 角度の種類 | 定義 | 主な用途・特徴 |
| 直角 | 90° | 最も一般的で基礎的な角度。製品の組み立て精度に直結します。 |
| 鋭角 | 90°未満 | シャープで洗練された外観を求められる製品に使用。プレーナー加工やシカル曲げといった特殊な技術が必要です。 |
| 鈍角 | 90°より大きい | 緩やかなカーブや特定の機能(部品のはめ込みなど)を持たせるために使用されます。 |
角の丸み(R)
加工された角には、意図的にまたは加工の性質上、わずかな丸みが生じます。このRの大きさは、製品の強度や安全性を決定する重要な要素です。
Rの役割は次の通りです。
| 役割 | 説明 |
| 強度 | 鋭利な角は応力が集中しやすいため、丸みをつけることで応力を分散させ、製品の亀裂や破損を防ぎ、強度を向上させます。 |
| 安全性 | 製品の角を丸めることで、使用者が接触した際に怪我をするリスクを減らします。 |
| デザイン | 丸みの大きさや形状は、製品の見た目の印象を大きく左右し、やわらかさや洗練された雰囲気を演出します。 |
板金の曲げ加工の見積での損をしない方法の記事を紹介します。
a角、b角、c角の関係性
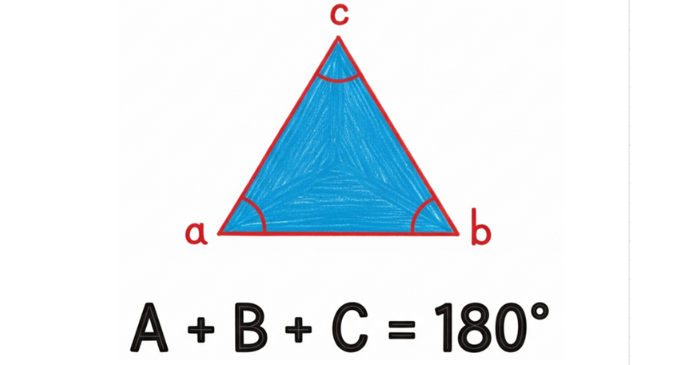
三角形の内角の合計は180度です。これは、a角、b角、c角が三角形の内角である場合に当てはまります。具体的には、a角 + b角 + c角 = 180度という関係性が成り立ちます。
また、2つの平行線に1つの直線が交わる場合、同位角と錯角の性質を理解することが重要です。同位角は同じ位置関係にある角で等しく、錯角もまた等しい関係にあります。
さらに、2つの直線が交わる際にできる対頂角は、常に等しいという性質を持っています。これらの関係性を知ることは、様々な幾何学の問題を解く上で非常に役立ちます。それでは詳細を見ていきましょう。
三角形における角の合計
三角形の3つの内角、つまりa角、b角、c角の合計は、常に180度になります。これは三角形の種類にかかわらず共通の性質であり、直角三角形、鋭角三角形、鈍角三角形など、どのような三角形でも変わりません。
たとえば、直角三角形では、1つの角が90度なので、残りの2つの角を足すと90度になります。この基本的な性質を理解することは、図形の問題を解く上で非常に重要です。
同位角と錯角の関係
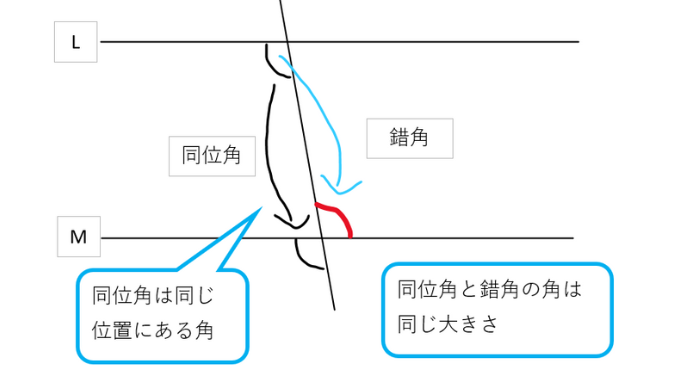
2本の平行な線に1本の線が交わるとき、同位角と錯角という関係を持つ角が生まれます。同位角は、同じ位置にある角のペアで、その大きさは常に等しくなります。
一方、錯角は、Z字形を描くような対角線上に位置する角のペアで、こちらも同じく大きさが等しいという性質を持っています。これらの関係性を知っておくことは、幾何学の問題を解く上で非常に重要です。
対頂角の性質
2つの直線が交わると、向かい合ってできる角のペアを対頂角と呼びます。対頂角は、常に大きさが等しいという性質があります。たとえば、アルファベットの「X」を想像してみてください。向かい合う2つの角が対頂角の関係にあり、その角度は同じです。
この性質は、関連する幾何学の問題を解く上で非常に重要な基礎知識となります。
実生活におけるa角、b角、c角の応用

私たちが日常で知っている様々な角の知識は、多くの分野で必要とされます。例えば、建築では、建物の安全性と美しさを両立させるために、材料の加工時に角のデザインが構造に大きな影響を与えます。
さらに、家具の設計においても、機能性や視覚的なバランス、ブランドイメージを考慮した上で、どの角度を使用するか計算する必要があるのです。このように、一見単純な角の概念は、様々な技術やデザインに深く関連しています。それでは詳細を見ていきましょう。
建築における角の利用
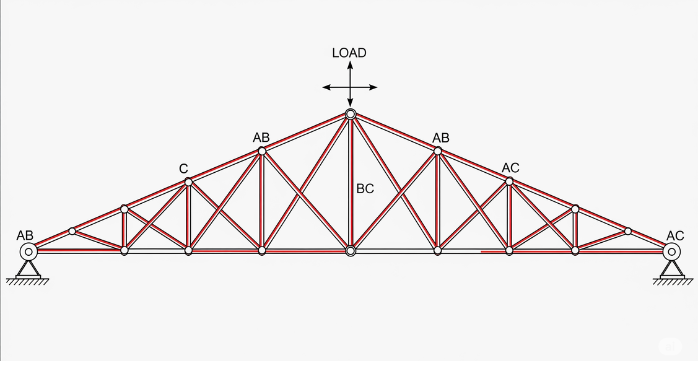
建築において、角はデザインと安全性の両方で重要な役割を果たします。建物の構造的な安定性を保つためには、部材を接合する際の角度、例えば直角や特定の鋭角が不可欠です。
また、ガラスや金属などの材料は、それぞれの特性を活かした加工技術で特定の角度に仕上げられます。これらの角のデザインは、見た目の美しさだけでなく、耐久性にも深く関わっており、建築物の品質を左右する重要な要素です。
金属加工における角の利用

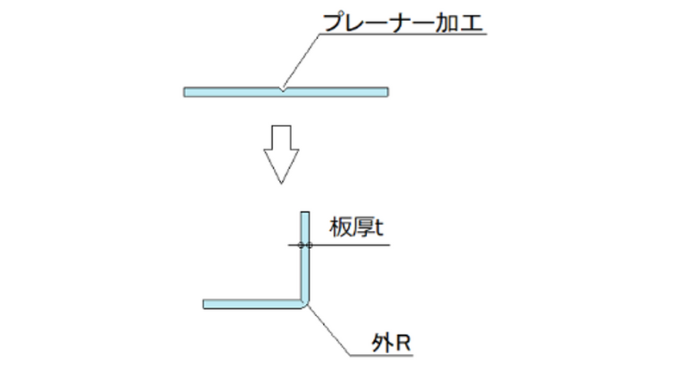
金属板の曲げ加工において、プレーナー加工(シカル曲げ加工)は、特に鋭い角度や複雑な形状を形成する際に重要な技術です。この加工方法では、V溝の深さによって「A角」「B角」「C角」という3種類の角度に分類されます。
A角は最もV溝が浅く、緩やかな角度の曲げ加工に使用されます。B角は一般的な建具などで使用される角度で、標準的なV溝の深さです。そして、C角はV溝が最も深く、外Rが小さい順に分類され、よりシャープな角度の曲げが必要な場合に使用されます。
これらの角度の分類を理解することは、プレーナー加工の精度と効率を高めるために不可欠な知識となります。
A角B角C角は、厳密なJIS規格などではなく、加工業界内で慣習的に使われる分類であり、会社や工場によって定義が異なる場合があります。しかし、一般的な傾向として以下のように理解されています。
リョーユウ工業ではV溝が最も深く、外Rが小さい溝をA角と定義し、一般的な建具などで使用される深さをB角と定義しております。
曲げ加工の基本と最適な業者選びについての記事を紹介します。
デザインでの角の重要性

デザインにおいて、角は製品の印象を大きく左右します。例えば、シャープな角は先進性や信頼感を演出し、自動車やスマートフォンのデザインに多用されます。

一方、丸みのある角は、親しみやすさや優しさを表現し、子供向け製品や家具によく見られます。このように、角の使い分けは、ブランドイメージを形作る上で非常に必要な要素です。機能性と美しさの両立を意識しながら、製品の特性に合った角のデザインが選ばれています。
角度計算のテクニック

角度の計算には、三角関数の使用が不可欠です。直角三角形の辺の比率から角度を導き出すために、sin、cos、tanを使用します。それで詳しく見ていきましょう。
角度三角関数の利用法
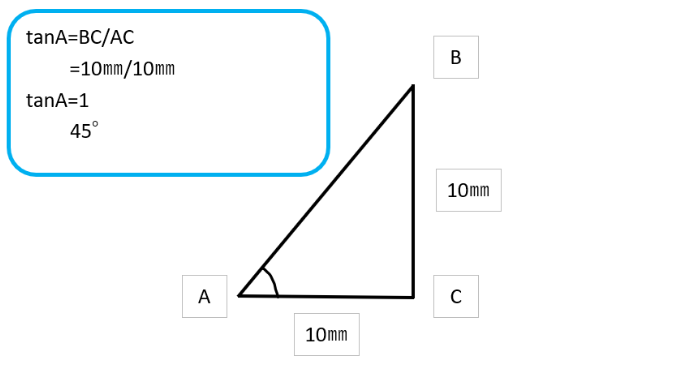
角度を求める計算には、三角関数の使用が不可欠です。直角三角形において、sin(サイン)、cos(コサイン)、tan(タンジェント)は、辺の比率から角度を導き出すために使用されます。
例えば、直角三角形の2つの辺の長さが分かれば、tan を使用して未知の角度を計算できます。このように、三角関数の基本的な定義を理解し、その使用方法をマスターすることで、複雑な角度計算も容易になります。
角度の変換とその計算
角度の単位には度とラジアンがあり、これらを相互に変換することは、計算を行う上で非常に重要です。180度がπラジアンに相当するという関係性を参考に、変換を計算します。
たとえば、90度はπ/2ラジアン、360度は2πラジアンとなります。三角関数などを用いる計算では、ラジアンを使用することが一般的であり、この変換を理解しておくことは不可欠です。
問題解決のための角度計算例
ある木の高さを知りたいとします。木から10メートル離れた地点から木のてっぺんを見上げた角度が45度でした。この場合、三角関数を使用して木の高さを計算できます。
この問題の解法は、tan45°=高さ/10mという式を立て、計算することです。tan45°=1なので、木の高さは10メートルだと分かります。このような応用例を知っておくことで、関連する情報をより深く理解し、質問にも答えられるようになります。
リョーユウ工業にご相談ください
リョーユウ工業では、主にシャーリング(切断)加工、タレットパンチ加工、プレーナー加工、レーザー加工、曲げ加工、面取り加工、溶接加工を行っています。塗装に関しても協力会社を通じて対応することが可能です。
リョーユウ工業の技術
リョーユウ工業は、年間50,000件もの加工実績があり、幅広い素材や形状に対応できることが強みです。また、最新の設備を導入しており、高精度な加工が可能です。さらに、小ロットから大ロットまで対応できるため、様々なニーズに対応できます。
- シャーリング(切断)加工
- タレットパンチ加工
- プレーナー加工
- レーザー加工
- 曲げ加工
- 面取り加工
- 溶接加工
他社で断られた案件でも、リョーユウ工業なら解決できるかもしれません。リョーユウ工業に依頼しても駄目なら他でもできない最大の信頼をもらえる会社を目指しています。
a角b角c角まとめ
日常生活に潜む角の知識は、建築やデザイン、金属加工、数学の学習に役立ちます。この記事では、まずa角、b角、c角を三角形の頂点の角度として定義し、その関係性(合計180度)を解説しました。また、同位角や対頂角といった幾何学の基礎も紹介しました。
角度の計算には、三角関数が不可欠であり、度とラジアンの変換方法や、問題解決のための応用例についても詳しく解説しました。これらの知識を身につけることで、物事の理解が深まるでしょう。
金属加工の豆知識一覧に戻る